Körper berechnen

Körper berechnen! Wenn dieses Thema im Unterricht dran kommt bin ich immer froh, dass wir jetzt nicht so etwas wie Therme behandeln.

Bei der Berechnung von Körpern spielt das ,,3D-Denken’’ eine wichtige Rolle. Das ist meist relativ einfach, aber wenn dann auch noch die ganzen Formeln dazu kommen fängt bei den meisten der Kopf schon an zu dampfen, denn wer (ausgenommen der Mathelehrer oder die Mathelehrerin) soll sich denn den ganzen ,,Krams’’ merken?

Dazu kann man sich zum Beispiel ein Lesezeichen oder Klebchen in seine Formelsammlung kleben, damit man die Übersicht behält (sofern eine Formelsammlung vorhanden ist).

Am besten hilft es immer wieder mit den Formeln zu rechnen und auch viele abwechslungsreiche Aufgaben zu lösen.

Navigation

Würfel berechnen

Quader berechnen

Dreiecks – Prisma berechnen

Pyramide mit quadratischer Grundfläche berechnen

Pyramide mit rechteckiger Grundfläche Berechnen

Pyramidenstumpf berechnen

Regelmäßigen Tetraeder berechnen

Zylinder berechnen

Kegel berechnen

Kegelstumpf berechnen

Kugel berechnen

Würfel berechnen:

Grundfläche:

$G=a^{2}$

$G=a\cdot a$

Oberfläche:

$O=6\cdot a$

Volumen V:

$V=a^{3}$

$V=a\cdot a\cdot a$

Diagonale:

$d=\sqrt {3}\cdot a$

Quader berechnen:

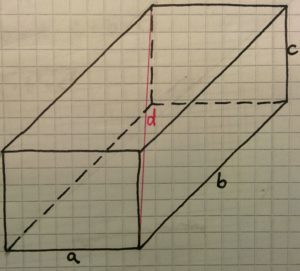
Volumen:

$V=a\cdot b\cdot c$

Grundfläche:

$G=a\cdot b$

Oberfläche:

$O=2\cdot \left( a\cdot b+a\cdot c+b\cdot c\right)$

Diagonale:

$d=\sqrt {a^{2}+b^{2}+c^{2}}$

Dreiecks – Prisma berechnen:

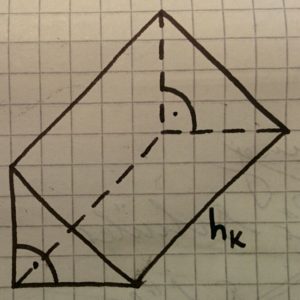
Volumen V:

$V=G\cdot h$

Die Grundfläche kann ein Dreieck, ein Viereck oder allgemein ein Vieleck sein. Als Körperhöhe wurde oben die Bezeichnung hk gewählt (zum unterscheiden der Körperhöhe von der Höhe der Grundseite).

Grundfläche:

Die Grundfläche hängt immer davon ab welche Fläche als Grundfläche angegeben ist. Wenn z.B. ein Quadrat angegeben ist, dann rechnet man für die Grundfläche G = a² aber wenn die Grundfläche ein Dreieck ist, dann rechnet man erst die Grundfläche des Dreiecks aus und dann nimmt man sie mal die Höhe und erhält somit das Volumen.

Oberfläche:

$O=2\cdot G+M$

Die Mantelfläche M sind die Seiten die quasi als Mantel um den Körper drum sind. Die Seiten, die keine Grundfläche sind.

Pyramide mit quadratischer Grundfläche berechnen:

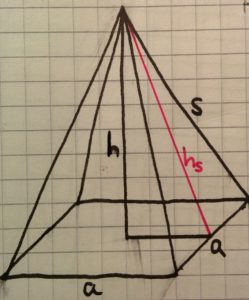
Volumen V:

$V=\dfrac {1}{3}\cdot G\cdot h$

$V=\dfrac {1}{3}\cdot a^{2}\cdot h$

Grundfläche G:

$G=a^{2}$

Mantelfläche M:

$M=2\cdot a\cdot h_{s}$

Oberfläche O:

$O=a\cdot \left( a+2\cdot hs\right)$

$O=G+M$

Pyramide mit rechteckiger Grundfläche Berechnen:

Volumen V:

$V=\dfrac {1}{3}\cdot G\cdot h=\dfrac {1}{3}\cdot a\cdot b\cdot h$

Höhe a:

$h_{a}=\sqrt {h^{2}+\left( \dfrac {b}{2}\right) ^{2}}$

Höhe b:

$h_{b}=\sqrt {h^{2}+\left( \dfrac {h}{2}\right) ^{2}}$

Grundfläche G:

$G=a\cdot b$

Mantelfläche M:

$M=a\cdot h_{a}+b\cdot h_{b}$

Oberfläche O:

$O=a\cdot b+a\cdot h_{a}+b\cdot h_{b}$

$O=M+G$

Pyramidenstumpf berechnen:

Deckfläche D:

$D=a_{1}\cdot b_{1}$

Grundfläche G:

$G=a_{2}\cdot b_{2}$

Volumen V:

$V=\dfrac {1}{3}\cdot h\cdot \left( G+\sqrt {D}\cdot G+D\right)$

Höhe a:

$h_{a}=\sqrt {h^{2}+\left( b_{2}-b_{1}\right) ^{2}:4}$

Höhe b:

$h_{b}=\sqrt {h^{2}+\left( a_{2}-a_{1}\right) ^{2}:4}$

Mantelfläche M:

$M=\left( b_{1}+b_{2}\right) \cdot h_{b}+\left( a_{1}+a_{2}\right) \cdot h_{a}$

Oberfläche O:

$O=a^{2}_{1}+2\cdot \left( a_{1}+a_{2}\right) \cdot h_{s}+a^{2}_{2}$

$O=M+G+D$

Regelmäßigen Tetraeder berechnen:

Höhe a:

$h_{a}=\dfrac {\sqrt {3}}{2}\cdot a$

Höhe:

$h=\sqrt {\dfrac {1}{2}}\cdot a$

$h=\dfrac {\sqrt {6}}{3}\cdot a$

Volumen V:

$V=\dfrac {1}{3}\cdot \dfrac {1}{2^{b}}a\cdot h$

$V=\dfrac {\sqrt {2}}{12}\cdot a^{3}$

Oberfläche O:

$O=4\cdot \dfrac {1}{2}\cdot a\cdot h_{a}$

$O=\sqrt {3}\cdot a^{2}$

Zylinder berechnen:

Volumen V:

$V=G\cdot h$

$V=\pi \cdot r^{2}\cdot h$

Grundfläche G:

$G=\pi \cdot r^{2}$

Mantelfläche M:

$M=2\cdot \pi \cdot r\cdot h$

Oberfläche O:

$O=2\cdot G+M$

$O=2\cdot \pi \cdot r^{2}+2\cdot \pi \cdot r\cdot h$

Kegel berechnen:

Volumen V:

$V=\dfrac {1}{3}\cdot G\cdot h=\dfrac {1}{3}\cdot \pi \cdot r^{2}\cdot h$

Grundfläche G:

$G=\pi \cdot r^{2}$

Schräge s:

$S=\sqrt {r^{2}+h^{2}}$

Mantelfläche M:

$M=\pi \cdot r\cdot s$

Oberfläche O:

$O=\pi \cdot r\cdot \left( r+s\right)$

$O=M+G$

Kegelstumpf berechnen:

Volumen V:

$V=\dfrac {1}{3}\cdot \pi \cdot h\cdot \left( r^{2}+r\cdot R+R^{2}\right)$

Mantellinie m:

$m=\sqrt {h^{2}+\left( R-r\right) ^{2}}$

Mantelfläche M:

$M=\pi \cdot m\left( r+R\right)$

Deckfläche D:

$D=\pi \cdot r^{2}$

Grundfläche G:

$G=R^{2}\cdot \pi$

Oberfläche O:

$O=M+G+D$

Kugel berechnen:

Durchmesser d:

$2\cdot r$

Radius r:

$t=\dfrac {d}{2}$

Volumen V:

$V=\dfrac {4}{3}\cdot \pi \cdot r^{3}$

Oberfläche O:

$O=4\cdot \pi \cdot r^{2}$

Loading ...

Körper berechnen

Navigation

Würfel berechnen:

Quader berechnen:

Dreiecks – Prisma berechnen:

Pyramide mit quadratischer Grundfläche berechnen:

Pyramide mit rechteckiger Grundfläche Berechnen:

Pyramidenstumpf berechnen:

Regelmäßigen Tetraeder berechnen:

Zylinder berechnen:

Kegel berechnen:

Kegelstumpf berechnen:

Kugel berechnen:

Ähnliche Beiträge

Schreibe einen Kommentar Antworten abbrechen