Die Wahrscheinlichkeitsrechnung – oftmals auch Stochastik genannt – ist für die meisten Schüler und Schülerinnen eines der schlimmsten Kapitel der Mathematik.
Die Wahrscheinlichkeitsrechnung oder Wahrscheinlichkeitstheorie ist ein umfangreiches Kapitel im Bereich Mathe. Daher habe ich das Thema in verschiedene Themen unterteilt. Zunächst sehen wie uns wichtige Grundbegriffe an und wenden uns dann Themen wie dem Binomialkoeffizient, dem Urnenmodell und vielem mehr dazu. In dem Bereich gilt es auch Begriffe wie Augenzahl, Ereignismenge und vieles mehr kennenzulernen.
Der Ereignisbaum der Wahrscheinlichkeitsrechnung
In unserer heutigen Zeit sind Vorhersagen und Wahrscheinlichkeiten im Leben fest etabliert, aber ohne die Rechnungen dahinter wären diese nicht möglich. Ein Beispiel ist z.B. Poker: Hier gibt es nur eine begrenzte Anzahl von Karten im Ganzen Spiel und deshalb kann man sich weitestgehend ausrechnen welche Karte auf der Hand des Spielers liegt, wenn die anderen auf dem Tisch liegen und man selber noch Karten hat. Und noch ein kleines Beispiel: „Kopf oder Zahl?“ heißt es oftmals, wenn eine Münze geworfen wird. Auf welcher der beiden Seiten die Münze landet, wisst ihr natürlich nicht. Nur eine Wahrscheinlichkeit kann angegeben werden. Es gibt zwei Seiten: Kopf oder Zahl. Somit ist die Wahrscheinlichkeit für Kopf 1/2 (=50%) und für Münze auch 1/2 (=50%). Und das bringt uns zum Ereignisbaum. Das Beispiel zur Wahrscheinlichkeitsrechnung mit der Münze von eben zeichnen wir in einen Ereignisbaum ein. Es gibt zwei Möglichkeiten ( Kopf, Zahl ) die bei einem Wurf eintreten können, folglich gibt es zwei Pfade. Die Wahrscheinlichkeit ist 1/2 für Kopf und 1/2 für Zahl, diese Werte werden an die Pfade geschrieben. Aber seht selbst:
Man kann alle Möglichkeiten, die existieren, zu einer Lösungsmenge „L“ zusammenfassen. Für unseren Fall wäre diese: L = { Kopf, Zahl }.
Ich habe hier eine Strichliste zu dem Münzwurf erstellt:
| Ergebnis | Striche | absolute Häufigkeit |
| Kopf |  | 21 |
| Zahl |  | 19 |
Die erste Spalte zeigt das Ergebnis an. In der zweiten Zeichnen wir die Anzahl ein, die wir dann für die Spalte ganz rechts abzählen. In unserem Fall wurden 21 mal Kopf und 19 mal Zahl geworfen. Es gab also 40 Wurfversuche. Sicherlich fragen sich jetzt einige: Wieso ist die Anzahl von Wappen und Zahl nicht gleich? Schließlich haben wir die Wahrscheinlichkeit mit 1/2 für Wappen und Zahl angegeben. Somit hätten wir bei 40 Versuchen eigentlich 20 Kopf und 20 Zahl erreichen müssen? Die Antwort: Wir geben hier eine Wahrscheinlichkeit an. Würden wir statt 40 Versuchen nun 400 Versuche machen, würden wir recht nahe an eine gleiche Verteilung ran kommen. Ihr solltet also sehr viele Versuche durchführen, um ein gutes Ergebnis zu bekommen. Das ist aber keine Aufforderung jetzt den ganzen Tag nur Münzen zu werfen.
Mehrstufige Experimente
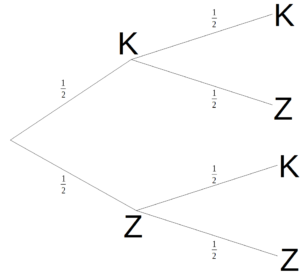
Manchmal will man jedoch nicht Wissen, ob Kopf oder Zahl bei einem Münzwurf fällt, sondern ob man zweimal Kopf oder Zahl hintereinander wirft. So etwas wird als mehrstufiges Experiment bezeichnet. Schau dir einmal den folgenden Ereignisbaum an, darunter findest du dann einige Erklärungen.
Wir beginnen ganz links. Soll nun Kopf-Kopf fallen, folgen wir dem Pfad ganz oben bis zum Ende ( K ; K ). Soll hingegen erst Zahl, dann Wappen fallen, gehen wir zu Beginn den Pfad nach unten ( Z ) und dann den Pfad zum Kopf ( K ). Die Wahrscheinlichkeit beträgt wie auch beim einstufigen Experiment hier 1/2. Wollen wir nun die Wahrscheinlichkeit berechnen, dass ein gewisser Pfad eintritt, müssen wir einfach die jeweiligen Werte miteinander multiplizieren. Für den Fall Kopf-Kopf wäre dies die Gleichung:
![]()
Das kann man jetzt auf alle möglichen Beispiele beziehen und anwenden. Die Menge der Pfade ändert sich natürlich wenn sich sie Anzahl der Möglichkeiten ändert, z.B. wenn 3 Kugeln mit verschiedenen Farben in einer Schüssel sind oder ähnliches.
Das sind alles sehr simple Beispiele der Anwendung. In den Klausuren werden komplexere Aufgaben abgefragt, dennoch wird es kein Problem geben, wenn du genug übst und die ganze Materie verstehst.