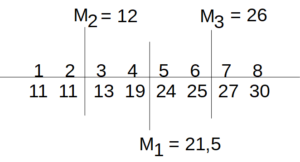Ein Boxplot ist ein Diagramm, das zur grafischen Darstellung der Verteilung der Daten sehr hilfreich ist. Im Klartext: Man kann sehen, wenn man z.B. eine Umfrage gemacht hat, in dem Diagramm sehen, wo die meisten Daten sind also in welche Richtung die Meinungen der Befragten hingehen.
Ich habe hier ein geeignetes Beispiel, welches typische Aufgabenstellungen enthält, gegeben:
Schülerinnen und Schüler wurden zu den monatlichen Kosten für die Handys befragt.
Jungen: 19€; 24€; 11€; 30€; 13€; 27€; 25€; 11€
Mädchen: 12€; 45€; 15€; 50€; 10€; 12€; 15€; 43€; 5€; 7€; 42€; 8€;
Aufgaben:
a) Stelle die Daten in einem zweiseitigen Stängel-Blätter-Diagramm dar.
b) Zeichne jeweils einen Boxplot für die angegebenen monatlichen Handykosten der Jungen und der Mädchen.
c) Welche Darstellungsform hältst du für aussagekräftiger? Begründe deine Meinung.
d) Gib sieben Daten an, deren Median 5,00€ und deren arithmetisches Mittel 9,00€ ist.
Vorgehensweise:
a)
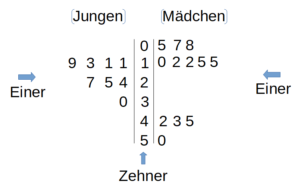
Wir können ein Stängel-Blätter-Diagramm Zeichnen und die verschiedenen Werte eintragen:
In der ersten Spalte sind die „Einer“der Jungen eingetragen dann kommen die „Zehner“ und zu guter Letzt die „Einer“ der Mädchen.
Die Einer und Zehner kann man sich so vorstellen: z.B. 23 (2 ist der Zehner und 3 ist der Einer); 45 (4 ist der Zehner und 5 ist der Einer)
In dem Diagramm können wir gut sehen, dass mehr Mädchen als Jungen befragt wurden. Bei den Mädchen kann man außerdem einen höheren Anteil an Teureren Handyverträgen feststellen.
b)
Diese Aufgabe ist etwas umfangreicher.
1. Werte nach der Größe Ordnen:
Jungen:
| 1. | 2. | 3. | 4. | 5: | 6. | 7. | 8. |
| 11 | 11 | 13 | 19 | 24 | 25 | 27 | 30 |
| 1. | 2. | 3. | 4. | 5. | 6. | 7. | 8. | 9. | 10. | 11. | 12. |
| 5 | 7 | 8 | 10 | 12 | 12 | 15 | 15 | 42 | 43 | 45 | 50 |
2. Es ist Zeit Die Mittelwerte zu bestimmen:
Wir brauchen von der „Jungen-Tabelle“ drei Mittelwerte (M1, M2 und M3). Wir bestimmen also erst mal den Mittelwert der „Jungen-Tabelle“ und dann jeweils die Mittelwerte der 2 übrig bleibenden Hälften.
Den Mittelwert ist der wert, der genau in der Mitte der Tabelle ist. Da wir in dem Beispiel der Jungen 8 Werte haben, wären die Werte in der Mitte die Nummer 4: 19 und die Nummer 5: 24. Tritt dieser Fall ein, musst du keine Panik kriegen, sondern die beiden Werte nehmen (19, 24), sie addieren und dann durch zwei teilen. So hast du den genauen Mittelwert der Tabelle herausbekommen, obwohl am Anfang zwei Werte genau in der Mitte waren.
Der Mittelwert (M1) ist übrigens 21,5.
Jetzt hast du die Tabelle schon in zwei Teile geteilt und nun musst du diese Zwei Teile jeweils auch in zwei Teile teilen. Nutze einfach das gleiche Prinzip, welches du gerade eben benutzt hast. Am Ende müsstest du drei Mittelwerte haben: M1 = 21,5; M2 = 12 und M3 = 26.
Hier nochmal eine Veranschaulichung:
Jetzt fangen wir mit dem Boxplot an:
Erstelle eine Strecke von deinem Kleinsten Wert bis zu deinem Größten Wert. dann trägst du die Mittelwerte auf der Stecke ab und verbindest sie mit einem Kasten. Im folgenden Bild siehst du was ich meine.
Nun haben wir einen Boxplot erstellt. Im Kasten befinden sich die meisten Daten/Werte und außerhalb sind recht wenig Daten/Werte (Die Daten/Werte sind nur schematisch in den Boxplot eingezeichnet und dienen nur zur Veranschaulichung).
c)
Nun, das zweiseitige Stängel-Blätter-Diagramm kann man viel schneller aufzeichnen und bekommt somit auch relativ schnell einen Überblick über die Verteilung der Daten/Werte. Mit dem Boxplot kann man die Daten Anschaulicher und exakter Präsentieren und ist auch bei größeren Mengen auf der sicheren Seite. Ich für meinen Teil finde das zweiseitige Stängel-Blätter-Diagramm besser, weil es einfach schneller geht. Ich kann mir aber vorstellen, dass man in Aufgaben eher den Boxplot benutzen muss, denn das zweiseitigen Stängel-Blätter-Diagramm ist ja echt keine große Herausforderung und wird vielleicht nur mal vorher zur Vorbereitung auf den Boxplot genutzt.
Ich wünsche dir noch einen schönen Tag und viel Erfolg bei der nächsten Klausur!