Es gib 3 wichtige Zahlensysteme in der Informatik.
- Binärsystem
- Dezimalsystem
- Hexadezimalsystem
Binär
Das Binäre Zahlensystem wird binär genannt, weil es nur 2 Zeichen hat, nämlich 0 und 1.
Zahlenbeispiel: 100001101001 (2)
Umrechnung ins Hexadezimalsystem
Dezimal
Das Dezimalsystem hat genau 10 Zeichen:
0, 1, 2, 3, 4, 5, 6, 7, 8 und 9
Zahlenbeispiel: 42 (10)
Hexadezimal
Das Hexadezimalsystem hat 16 Zeichen:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
Die Buchstaben stehen dabei für 10 – 15
- A = 10
- B = 11
- C = 12
- D = 13
- E = 14
- F = 15
Zahlenbeispiel: 26FA (16)
Umrechnung
Binär > Dezimal
Beispiel: 10101001 (2)

Erklärung
- Man muss die Stellen zählen, die hinter der zu berechnenden Zahl stehen. Bei der ganz linken 1 wären das 7.
- Dann muss man 2^die Zahl, die man herausbekommt nehmen. In dem Fall für die ganz linke 1 wäre das dann 2^7.
- Am Ende muss man dann mal 0 oder 1 machen. Je nach dem was da steht. Im Fall für die ganz linke 1 ist das dann mal 1.
- Heraus bekommt man dann 2^7 mal 1
- Das wiederholt man dann für jede Ziffer in der Binären Zahl und rechnet alles zusammen.
Das Ergebnis für die Beispielaufgabe würde 169 ergeben.
Dezimal > Binär
Beispiel: 42 (10)
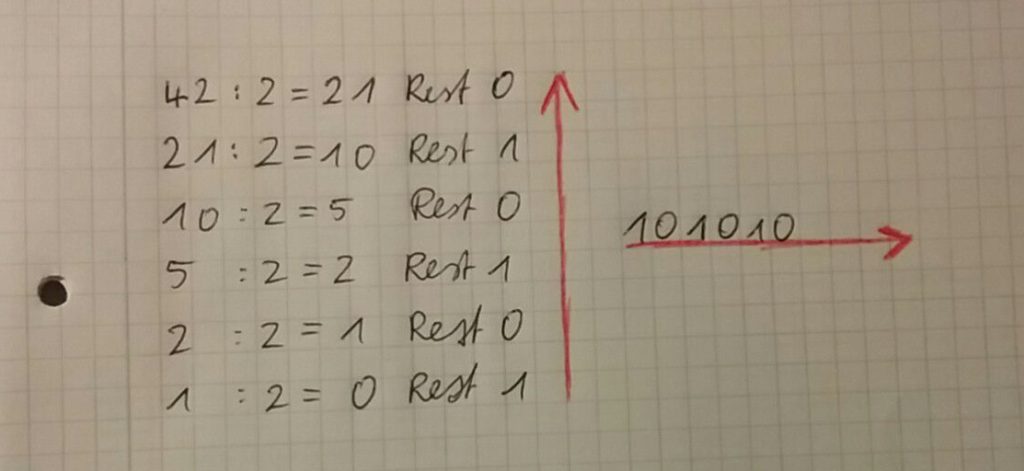
dezimal in binär
Erklärung
Hierbei muss man die Anfangszahl immer so lang durch 2 teilen bis es nicht mehr geht. Wenn eine ,5 Zahl herauskommt schreibt man einen Rest 1 hin und wenn eine Zahl ohne Kommastelle herauskommt schreibt man den Rest 0 hin.
Anschließend nimmt man die Zahl von unten nach oben und schreibt sie von links nach rechts auf.
Binär > Hexadezimal
Beispiel: 1011000110 (2)
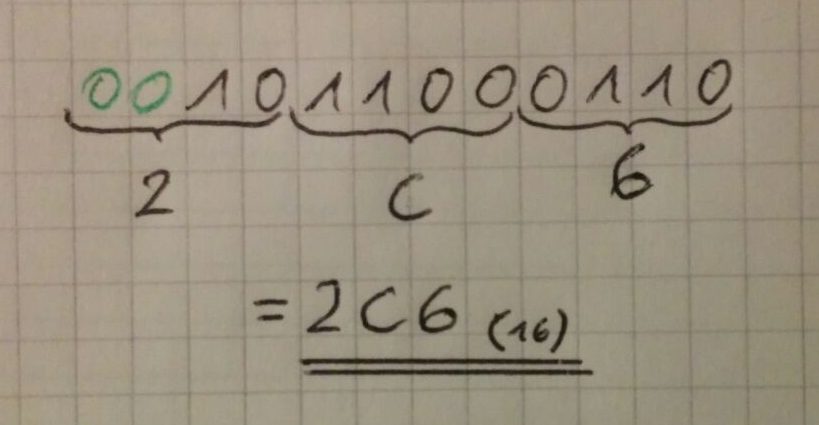
Erklärung
Man fängt von rechts an und nimmt immer vier Stellen der binären Zahl. Wenn man keine vier Stellen mehr hat, so wie vorne stellt man so viele nullen vor, damit es wieder 4 Stellen sind.
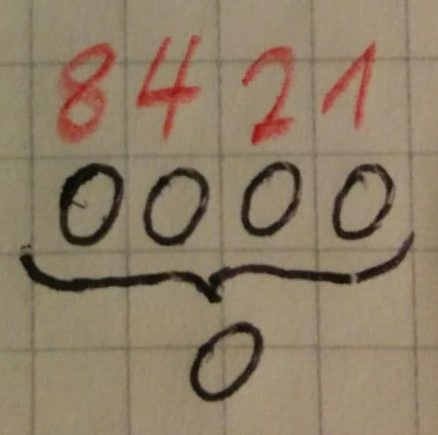
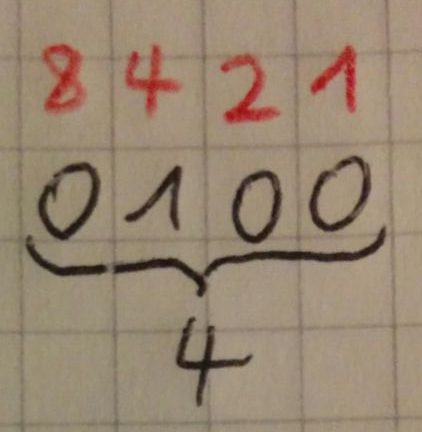
Es gibt verschiedene Wertigkeiten, die ich unten in den zwei Bildern näher erläutert habe. Diese treffen ein, wenn eine 1 an der Stelle steht. Wenn es mehrere gibt, rechnet man sie zusammen.
Hexadezimal > Binär
Beispiel: 7A (16)

Erklärung
Das gleiche wie bei binär zu hexadezimal bloß umgekehrt.
Super Erklärt.
hat mir sehr weitergeholfen.