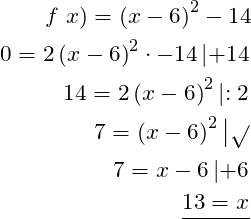In diesem Beitrag gehe ich auf die Technik ein, wie man die Schnittpunkte einer Parabel mit der y – und der x – Achse herausfinden kann.
Schnittpunkt Y – Achse
Normalform:
Wenn man die Normalform hat ist das Herausfinden des Schnittpunktes auf der Y – Achse ein Leichtes, denn man muss nur ablesen.
Beispiel Normalform:
Hierbei wäre der Schnittpunkt der y – Achse -17.
Beispiel Scheitelpunktsform:
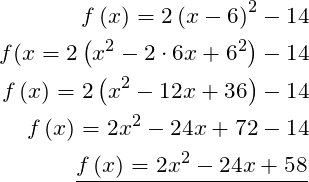
Bei diesem Beispiel wäre 58 der y – Achsenschnittpunkt.
Dies geht jedoch noch einfacher mit einer sofortigen Gleichsetzung von x = 0. Dieser Rechenweg ist zwar schneller, aber wenn die Aufgabenstellung eine Normalform verlangt völlig nutzlos, denn meist soll man dann mit der Normalform weiter rechnen.
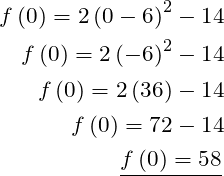
Schnittpunkt X – Achse
Normalform:
Wenn man die Normalform hat muss man zuerst die Formel null setzen. Das heißt aus dem 
eine Null machen, dann die ganze Formel durch die Zahl vor dem 
teilen.
Wenn man das gemacht hat kann man ohne Probleme die pq-Formel anwenden und die Nullstellen (Schnittpunkte der Parabel mit der x – Achse) herausfinden.
Scheitelpunktsform:
Bei der Scheitelform muss man die Formel wieder null setzen und die Klammer isolieren, sodass sie alleine auf einer Seite steht.
Beispiel Scheitelform:
