Der Grenzwert für 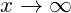 und
und 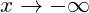
Den Grenzwert von Funktionen gegen ![]() und
und ![]() beschreibt man folgender Maßen:
beschreibt man folgender Maßen:
![]()
Wir nutzen die Funktion ![]() als Beispiel.
als Beispiel.
Vermutung
Eine Vermutung kann man z. B. durch einen Graphen aufstellen.
![]()
Testwerte
| 10 | 1,371 |
| 100 | 1,03 |
| 1000 | 1,003 |
Testfolge
Die Testfolge ist dafür da eine unendliche Menge in einen Grenzwert der Funktion einzusetzen.
![]()
![]()
Die Testfolge ![]() beinhaltet Alle natürlichen Zahlen.
beinhaltet Alle natürlichen Zahlen.
![]()
Funktionswertfolge
Die Testfolge ist nun in die Funktion, die es zu prüfen gilt, einzusetzen.
Bei ![]() würde das folgendermaßen aussehen.
würde das folgendermaßen aussehen.
![]()
Nun läuft ![]() gegen
gegen ![]()
![]()
![Rendered by QuickLaTeX.com \[= \lim_{n \to \infty}\frac{n(1+\frac{1}{n})}{n(1-\frac{2}{n})}\]](https://wissensplattform-schueler.de/wp-content/ql-cache/quicklatex.com-63ed515c55afda0ed252b23251937dfa_l3.png)
![Rendered by QuickLaTeX.com \[= \lim_{n \to \infty}\frac{1+\frac{1}{n}}{1-\frac{2}{n}}= \frac{1}{1} = 1\]](https://wissensplattform-schueler.de/wp-content/ql-cache/quicklatex.com-59b5f5bc72acb61e5044cde2033b971d_l3.png)
und es ist leicht zu sehen, dass der Grenzwert ![]() ist.
ist.
Allgemeine Testfolge
![]()
![]()
![Rendered by QuickLaTeX.com \[f(x_n)=\frac{x_n+1}{x_n-2}\]](https://wissensplattform-schueler.de/wp-content/ql-cache/quicklatex.com-217cd994c9a87c4f18d6291d27417f31_l3.png)
![Rendered by QuickLaTeX.com \[\lim_{x_n \to \infty}(\frac{x_n+1}{x_n-2})\]](https://wissensplattform-schueler.de/wp-content/ql-cache/quicklatex.com-bf952081a03d50f35ab9bc4e7d41fc7b_l3.png)
![Rendered by QuickLaTeX.com \[= \lim_{x_n \to \infty}\frac{x_n(1+\frac{1}{x_n})}{x_n(1-\frac{2}{x_n})}\]](https://wissensplattform-schueler.de/wp-content/ql-cache/quicklatex.com-959e37a3319514f0cb298a89a0ed0eab_l3.png)
![Rendered by QuickLaTeX.com \[= \lim_{x_n \to \infty}\frac{1+\frac{1}{x_n}}{1-\frac{2}{x_n}}= \frac{1}{1} = 1\]](https://wissensplattform-schueler.de/wp-content/ql-cache/quicklatex.com-55285e3068980629fbbbe453edafe315_l3.png)
Der Grenzwert an einer Stelle 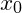
Den Grenzwert von Funktionen gegen ![]() beschreibt man folgender Maßen:
beschreibt man folgender Maßen:
![]()
Wir nutzen die Funktion ![]() als Beispiel und gucken uns den Grenzwert an der Stelle
als Beispiel und gucken uns den Grenzwert an der Stelle ![]() an.
an.
Vermutung
Eine Vermutung kann man z. B. durch einen Graphen aufstellen.
![]()
Testwerte
| 1,1 | 2,1 |
| 1,01 | 2,01 |
| 1,001 | 2,001 |
Testfolge
Die Testfolge ist dafür da eine unendliche Menge in einen Grenzwert der Funktion einzusetzen.
![]()
![]()
Die Testfolge ![]() hat den Grenzwert
hat den Grenzwert ![]() um der Stelle
um der Stelle ![]() nahe zu kommen.
nahe zu kommen.
![]()
Funktionswertfolge
Die Testfolge ist nun in die Funktion, die es zu prüfen gilt, einzusetzen.
Bei ![]() würde das folgendermaßen aussehen.
würde das folgendermaßen aussehen.
![Rendered by QuickLaTeX.com \[f(x)=\frac{(1+\frac{1}{n})^2-1}{1+\frac{1}{n}-1}\]](https://wissensplattform-schueler.de/wp-content/ql-cache/quicklatex.com-56546de2b8b6871d7419b2d62e9c70d1_l3.png)
Nun läuft ![]() gegen
gegen ![]()
![Rendered by QuickLaTeX.com \[\lim_{n \to \infty}\frac{(1+\frac{1}{n})^2-1}{1+\frac{1}{n}-1}\]](https://wissensplattform-schueler.de/wp-content/ql-cache/quicklatex.com-40f8de2c5bb7351f1854e353c6cfc797_l3.png)
![Rendered by QuickLaTeX.com \[= \lim_{n \to \infty}\frac{1+\frac{2}{n}+\frac{1}{n^2}-1}{1+\frac{1}{n}-1}\]](https://wissensplattform-schueler.de/wp-content/ql-cache/quicklatex.com-39cf2bf6155538c88c74524317ba027c_l3.png)
![Rendered by QuickLaTeX.com \[= \lim_{n \to \infty}\frac{\frac{2}{n}+\frac{1}{n^2}}{\frac{1}{n}}\]](https://wissensplattform-schueler.de/wp-content/ql-cache/quicklatex.com-838a79724993cab6ca9479528192aaf8_l3.png)
![]()
![]()
und es ist leicht zu sehen, dass der Grenzwert ![]() ist.
ist.
Allgemeine Testfolge
![]()
![]()
![Rendered by QuickLaTeX.com \[f(x_n)=\frac{{x_n}^2-1}{x_n-1}\]](https://wissensplattform-schueler.de/wp-content/ql-cache/quicklatex.com-86ffecb89298060d042fdacf58347f8d_l3.png)
![Rendered by QuickLaTeX.com \[\lim_{n \to \infty}\frac{{x_n}^2-1}{x_n-1}\]](https://wissensplattform-schueler.de/wp-content/ql-cache/quicklatex.com-26b45884e21068d1ef0677e12f97eece_l3.png)
![Rendered by QuickLaTeX.com \[= \lim_{n \to \infty}\frac{(x_n-1)(x_n+1)}{x_n-1}\]](https://wissensplattform-schueler.de/wp-content/ql-cache/quicklatex.com-ec5f3ac923d593e2da7b845c5c925a24_l3.png)
![]()