Logarithmusfunktion

Veröffentlicht am 19. Januar 202019. Januar 2020 by Simon

Beispiel

$f(x)=2^x \rightarrow green$

$y=2^x$

$x=\log_2 y$

$f^{-1}(x)=\log_2 x \rightarrow blue$

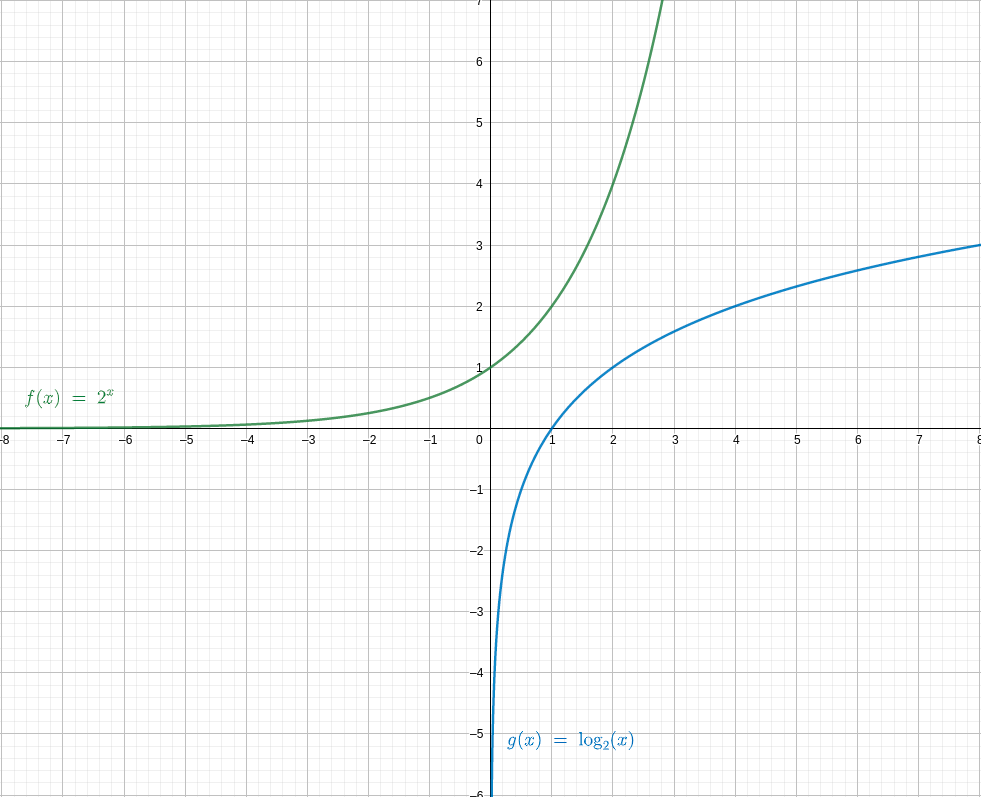
Allgemein

$f(x)=a^x$

$y=a^x$

$x=\log_a y$

$f^{-1}(x)=\log_a x$

Gleichung der Logorithmusfunktion

$f(x)=\log_a x$

$\mathbb{D}_f=x\in\mathbb{R}^+$

$\mathbb{W}_f=x\in\mathbb{R}$

Mithilfe von Logarithmen ist es möglich Exponentialgleichungen zu lösen.

Beispiel

$3^x=81$

$x=\log_3 81$

$x=4$

$4^x=16$

$x=\log_4 16$

$x=2$

Solche Gleichungen kann man auch mit anderen Arten von Logarithmen lösen.

Ähnliche Beiträge

Simon

Diese Webseite habe ich während meines Abiturs aufgesetzt und betrieben. Ich habe einige Themen, die mich besonders interessiert haben, in meinem Stil aufbereitet und veröffentlicht. Jetzt studiere ich Physik.

Beispiel

Allgemein

Gleichung der Logorithmusfunktion

Beispiel

Ähnliche Beiträge

Schreibe einen Kommentar Antwort abbrechen