Das Steigungsproblem
Es wird behandelt, welche Steigung die Stelle ![]() hat oder welche Stelle die angegebene Steigung besitzt.
hat oder welche Stelle die angegebene Steigung besitzt.
Stelle gegeben
Es wird die Tangentensteigung ![]() an der Stelle
an der Stelle ![]() gesucht. Die Steigung berechnet wird berechnet, indem
gesucht. Die Steigung berechnet wird berechnet, indem ![]() in
in ![]() eingesetzt wird.
eingesetzt wird.
![]()
Steigung gegeben
Es wird die Stelle ![]() gesucht an der sich die gegebene Steigung
gesucht an der sich die gegebene Steigung ![]() befindet. Dafür muss die erste Ableitung mit der Steigung
befindet. Dafür muss die erste Ableitung mit der Steigung ![]() gleichgesetzt werden und nach
gleichgesetzt werden und nach ![]() umgestellt werden.
umgestellt werden.
![]()
Das Steigungswinkelproblem
Hierbei wird beantwortet, welchen Steigungswinkel die Funktion an der Stelle ![]() hat.
hat.
Mithilfe des Arkustangens wird die herausgefundene Steigung in einen Winkel umgewandelt.
![]()
![]()
Das Extremalproblem
Klärung der Hoch- und Tiefpunkt einer Funktion ![]() .
.
Um den Hoch- oder Tiefpunkt einer Funktion ![]() zu finden muss die
zu finden muss die ![]() null gesetzt werden und das Ergebnis bzw. die Ergebnisse in
null gesetzt werden und das Ergebnis bzw. die Ergebnisse in ![]() eingesetzt werden. Wenn die Einsetzung in die 2. Ableitung ein negatives Ergebnis ausgibt, dann handelt es sich um einen Hochpunkt. Gibt sie jedoch einen positiven Wert auch handelt es sich um eine Tiefpunkt.
eingesetzt werden. Wenn die Einsetzung in die 2. Ableitung ein negatives Ergebnis ausgibt, dann handelt es sich um einen Hochpunkt. Gibt sie jedoch einen positiven Wert auch handelt es sich um eine Tiefpunkt.
![]()
![]() Hochpunkt
Hochpunkt
Um den y-Wert zu berechnen setzt man den beim Nullsetzen der 1. Ableitung gefundenen x-Wert in die Funktion ![]() ein.
ein.
![]()
Das Tangentenproblem
Die Gleichung der Tangente wird an der Stelle ![]() auf der Funktion
auf der Funktion ![]() gefunden.
gefunden.
Ansatz
![]()
Werte
![]()
![]()
![]()
n berechnen
![]()
![]()
Tangentengleichung
![]()
Das Schnittwinkelproblem
Schneiden sich die Graphen von ![]() und
und ![]() an der Stelle
an der Stelle ![]() , so bilden ihre Tangenten dort zwei Winkel
, so bilden ihre Tangenten dort zwei Winkel ![]() und
und ![]() miteinander.
miteinander.
Den kleineren der beiden Winkel bezeichnet man als Schnittwinkel ![]() von
von ![]() und
und ![]() an der Stelle
an der Stelle ![]() , wenn
, wenn ![]() gilt.
gilt.
1. Steigungswinkel 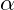 von
von 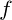 bei
bei 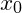
![]()
![]()
2. Steigungswinkel 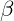 von
von  bei
bei 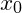
![]()
![]()
Winkelberechnung
![]()
Wenn ![]() dann ist der
dann ist der ![]() . Andernfalls ist der
. Andernfalls ist der ![]() .
.
Das Berührproblem
Es wird geprüft ob sich die Graphen von ![]() und
und ![]() nur in einem „treffen“.
nur in einem „treffen“.
Ansatz
Erst muss bewiesen werden, dass gleiche Funktionswerte existieren. Sie müssen sich ja in einem Punkt treffen um sich zu berühren. Es muss durch Gleichstellung der Funktionen die Stelle ![]() gefunden werden.
gefunden werden.
![]()
Nun muss bewiesen werden, dass die Funktionen an der vorher gefundenen Stelle ![]() die Gleiche Steigung haben. Dazu setze man diese in die ersten Ableitungen ein müsste die Gleichstellung eine wahre Aussage ergeben.
die Gleiche Steigung haben. Dazu setze man diese in die ersten Ableitungen ein müsste die Gleichstellung eine wahre Aussage ergeben.
![]()