Das Einheiten Umrechenen ist eine Angelegenheit, bei der viele Fehler zustande kommen, welche mit den folgenden Methoden vermeidbar sind.
Einheiten sind im Grunde genommen einfache Faktoren, welche mit zahlen Multipliziert oder dividiert werden. ![]() kann auch wie
kann auch wie ![]() notiert werden. Beides sagt das gleiche aus. So kann
notiert werden. Beides sagt das gleiche aus. So kann ![]() mit dem gleichen Prinzip auch wie
mit dem gleichen Prinzip auch wie ![]() notiert werden.
notiert werden.
Die folgende Tabelle ist auswendig zu lernen, damit die umrechnung von Statten gehen kann.
| Zehnerpotenzen | Präfix | | | Zehnerpotenzen | Präfix |
| da | | | d | ||
| h | | | c | ||
| k | | | m | ||
| M | | | µ |
Nun kann man die verschiedenen Präfixe mit ihren Zehnerpotenz-Werten austauschen und man ist fertig mit der umrechnung.
Bsp.: 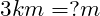
![]()
Wenn man nun in den quadratischen und kubischen Raum weitergehen will kann man das gerne tun, aber es ist eine entscheidende Änderung zu beachten.
Hierbei muss nämlich die Zehnerpotenz zusätzlich ins Quadrat oder Kubik genommen werden.
Bsp.: 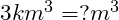
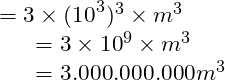
Bsp.: 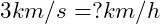
(1) 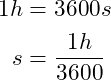
Wenn man ![]() ersetzt kommt man auf folgendes Ergebnis.
ersetzt kommt man auf folgendes Ergebnis.

Vorsicht
Diese Methode ist ausschließlich beim Präfix (Vorsilbe z. B.: bei km das k) der Einheit anwendbar und funktioniert NICHT bei den Suffixen (Nachsilbe z. B.: bei km das m)!