Die natürliche Exponentialfunktion

Veröffentlicht am 20. Januar 202020. Januar 2020 by Simon

Eigenschaften

$f(x)=e^x$ hat folgende Eigenschaften:

streng monoton steigend (f ist also umkehrbar)
stetig
differenzierbar
$\mathbb{W}= \mathbb{R}^+$
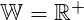
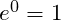$e^0=1$ und $e^1=e$
$f'(x)=e^x$

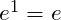
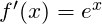
Umkehrfunktion

$f(x)=e^x$

$y=e^x$

$\ln y=x\ln e$ wobei $\ln e = 1$

$x=\frac{\ln y}{\ln e}$

$y=\frac{\ln x}{\ln e}$ wobei $\ln e = 1$

$y=\ln x$

$f^{-1}(x) = \ln x$

Nun haben wird die natürliche Logarithmusfunktion.

Wichtiger Satz

Wendet man die Umkehrfunktion $f^{-1}$ und die Funktion $f$ nacheinander auf $x$ an, dann entsteht $x$ .

$f(f^{-1}(x))=x$

Übertragung auf e-Funktion:

$e^{\ln x}=x$

$\ln e^x=x$

$x\ln e = x$

Beispiel

$f(x)=x^{\frac{1}{x}}=e^{\ln(x^{\frac{1}{x}})}$

Dies kann besonders bei Grenzwerten nützlich werden.

Entdeckung der Exponentialfunktion

$(1)$

$f(x)=2^x$

$f'(x)=0,7\cdot 2^x$

Irgendwo zwischen $0,7$ und $1,1$ muss $c=1$ liegen. Es muss also eine Funktion geben, die sich selbst als Ableitungsfunktion hat. Die Basis $a$ dieser Funktion wird mit $\mathrm{e}$ bezeichnet.

$(2)$

$f(x)=\mathrm{e}^x$

$f'(x)=1\cdot \mathrm{e}^x = \mathrm{e}^x$

$(3)$

$f(x)=3^x$

$f(x)=1,1\cdot 3^x$

Ähnliche Beiträge

Diese Webseite habe ich während meines Abiturs aufgesetzt und betrieben. Ich habe einige Themen, die mich besonders interessiert haben, in meinem Stil aufbereitet und veröffentlicht. Jetzt studiere ich Physik.

Schreibe einen Kommentar Antwort abbrechen