Plattenkondensator

Unter einem Plattenkondensator versteht man eine Anordnung von zwei leitenden Körpern beliebiger Form, die gegeneinander isoliert aufgestellt sind. Verbindet man einen der beiden Körper mit dem Minus-, den anderen mit dem Pluspol einer Spannungsquelle $u$ , so fließen auf die Körper Ladungen auf, die unterschiedliches Vorzeichen, aber den gleichen Betrag $Q$ haben. So können Ladungen gespeichert werden.

Viele Versuch haben ergeben, dass $Q \sim U$ ist, weshalb für jeden Plattenkondensator eine Proportionalitätskonstante gibt:

$C=\frac{Q}{U}$

Diese Konstante hat die Einheit $F$ (Farrad).

Ladung

Wenn man also die gespeicherte Ladung eines Plattenkondensators errechnen möchte muss man die Kapazität $C$ und die Spannung $U$ zwischen den Platten wissen und folgende Formel (auch bekannt als „Ku=Ku“-Regel) verwenden.

$Q=C\cdot U$

Hinweise

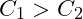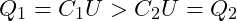Die Kapazität $C$ ist ein Maß für das Ladungsfassungsvermögen eines Kondensators. Werden nämlich zwei Kondensatoren unterschiedlicher Kapazitäten $C_1 > C_2$ an die gleiche Spannungsquelle $U$ angeschlossen, so fließt auf den Kondensator mit der größeren Kapazität wegen $Q_1 = C_1 \codt U > C_2 \codt U = Q_2$ der größere Ladungsbetrag auf.
Trägt man die Ladung eines Kondensators in einem U-Q-Diagramm gegen die Spannung $U$ an, so erhält man wegen $Q=C\dot U$ eine Ursprungsgerade mit der Steigung $C$ .

Kapazität

Man kann die Kapazität $C$ eines Plattenkondensators mit der Formel $C={\varepsilon _0} \cdot {\varepsilon _r} \cdot \frac{A}{d}$ berechnen. Der Herleitung widmen wir uns jetzt.

Um die Formel herzuleiten müssen wir bestimmte Größen finden, die die Kapazität des Plattenkondensators beeinflussen. Diese Größen müssen veränderbar sein. Deshalb nehmen wir den Flächeninhalt $A$ der Platten und den Abstand $d$ zwischen den Platten.

Flächeninhalt

Viele Versuche haben bei gleichem Abstand $d$ zwischen den Platten ergeben, dass die Kapazität $C$ und der Flächeninhalt $A$ direkt proportional zueinander sind. Zu vermuten ist: $C\sim A$ .

Das heißt $\frac{C}{A}$ ist bei konstantem Abstand $d$ konstant.

Abstand

Viele Versuche haben bei gleichem Flächeninhalt $A$ der Platten ergeben, dass die Kapazität $C$ und der Abstand $d$ indirekt proportional zueinander sind. Zu vermuten ist: $C\sim \frac{1}{d}$ .

Das heißt $C\cdot d$ ist bei konstantem Flächeninhalt $A$ konstant.

Auswertung

Abhängigkeit der Kapazität von den geometrischen Größen eines Plattenkondensators kann man nun in einer Beziehung zusammenfassen. Sie lauten

$C \sim A\;{\rm{bei}}\;d = const.$

und

$C \sim \frac{1}{d}\;{\rm{bei}}\;A = const.$

Wenn man beide Proportionalitäten zusammenfasst gilt

$C \sim A \cdot \frac{1}{d} = \frac{A}{d}$