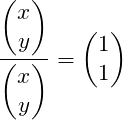Vektoren

Vektoren haben immer eine Länge und Richtung und werden als Pfeil bezeichnet $\vec{x}$ . Vektoren sind teil der Trigonometrie

Vektorielle Größen

Kraft $\vec{F}$
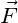
Geschwindigkeit $\vec{v}$
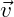
Beschleunigung $\vec{a}$
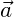
Impuls $\vec{p}$

Vektorschreibweise

(1) $\begin{equation*} \vec{v}=\begin{pmatrix} x \\ y \end{pmatrix}\end{equation*}$

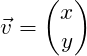
Dieser 2-dimensionale Vektor besteht aus zwei Komponenten $v_x$ und $v_y$ .

Rechenoperationen

Addition

(2) $\begin{equation*} \begin{pmatrix} x \\ y \end{pmatrix}+\begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 2x\\2y \end{pmatrix}\end{equation*}$

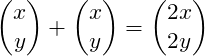
Subtraktion

(3) $\begin{equation*} \begin{pmatrix} x \\ y \end{pmatrix}-\begin{pmatrix} x \\ y \end{pmatrix}= \begin{pmatrix} -x\\-y \end{pmatrix}\end{equation*}$

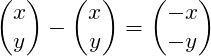
Multiplikation

(4) $\begin{equation*} \begin{pmatrix} x \\ y \end{pmatrix}\cdot\begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} x^2\\y^2 \end{pmatrix}\end{equation*}$

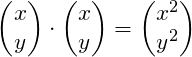
Division

(5) $\begin{equation*} \frac{\begin{pmatrix} x \\ y \end{pmatrix}}{\begin{pmatrix} x \\ y \end{pmatrix}}= \begin{pmatrix} 1\\1 \end{pmatrix}\end{equation*}$