Substitutionsverfahren

Veröffentlicht am 18. Januar 202027. Dezember 2020 by Simon

Beim Substitutionsverfahren substituiert man $x^2 = z$ , damit man eine Gleichung des 4. Grades lösen kann. Idem man eine Gleichung 4. Grades substituiert bekommt man eine quadratische Gleichung, die man mit der p-q-Formel berechnen kann.

Beispiel

$f(x)=x^4+2x^2-8$

Nun substituiert man $x^2 = z$

$f(x)=z^2+2z-8$

und kann die p-q-Formel benutzen um auf die beiden möglichen Lösungen der Variable $z$ zu kommen.

$\begin{equation*}\begin{split}{z}_{1/2}&=-\frac{p}{2} \pm \sqrt{ (\frac{p}{2})^2-q}\\{z}_{1/2}&=-1 \pm \sqrt{ 1^2+8}\\{z}_{1/2}&=-1 \pm 3\\{z}_{1}&=2\\{z}_{2}&=-4\end{split}\end{equation*}$

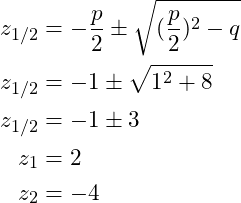
Jetzt muss man rücksubstituieren, denn $z_1$ und $z_2$ sind ja nicht die Lösungen der originalen Gleichung, sondern die der substituierten.

Es muss die Wurzel aus den Ergebnissen gezogen werden.

$x^2=2$

$x_1=\sqrt{2}$

$x_2=-\sqrt{2}$

$x^2=-4$

Die Wurzel aus eine negativen Zahl zu ziehen ist nicht möglich.

Wir haben nun zwei Lösungen für die originale Gleichung gefunden.

Ähnliche Beiträge

Diese Webseite habe ich während meines Abiturs aufgesetzt und betrieben. Ich habe einige Themen, die mich besonders interessiert haben, in meinem Stil aufbereitet und veröffentlicht. Jetzt studiere ich Physik.

1 Antwort zu “Substitutionsverfahren”

Pingback: Lösen von Gleichungen – Wissensplattform

Schreibe einen Kommentar Antworten abbrechen